[DB07] Relational Algebra_SELECT, JOIN, PROJECT 등
* 10.17 업데이트
해당 게시물은 한양대학교 컴퓨터소프트웨어학부 김상욱 교수님 데이터베이스시스템 온라인 강의를 듣고 정리한 자료입니다.
오류가 있다면 언제든 알려주세요!
● 해당 강의의 목표
1. relational algebra에 대해 배운다.
▪ relational algebra는 relational database로부터 원하는 정보를 끌어내는데 사용되는 operator 집합이다.
▪ relational algebra에 있는 operator에 대해 알아본다.
▪ relational algebra에서 query를 어떻게 쓰는지 알아본다.
◆ Relational Algebra
▪ relational model에서 사용되는 operation들의 집합이다.
▪ relational database에서 정보들을 retrieval, search하기 위한 요구를 명시하기 위해서 사용되는 operation들의 집합이다.
ex) "학생 database로부터 홍길동에 대한 주소를 검색해줘." 라고 요청하는 것을 retrieval request 또는 query라고 부르고, relational operator를 통해서 이를 표현한다.
▪ relational algebra로 정보가 retrieve된 결과는 하나의 relation으로 표현된다.
즉, database에 relational algebra를 통해서 검색된 결과는 다시 relation(table)이다. 다시! 검색 후에 나온 결과는 table이다.
▪ relational algebra operation types
1. SELECT
2. PROJECT
3. Set operations
4. JOIN
...
◆ SELECT Operation
▪ Format $\sigma_{<selection$ $condition>}(R)$
$R$이라는 이름을 가지는 table에서 조건에 만족하는 tuple만 골라줘.
▪ relation $R$로부터 condition c를 만족하는 일부의 tuple들을 고른다.
▪ c는 Boolean expression으로 구성된다.
- <attribute name> <comparison op> <constant value>
ex) grade > 3.5
- <attribute name> <comparison op> <attribute name>
ex) 수입 > 지출
▪ select operation에서 나오는 결과는 relation이고 $r$($R$)에서 c를 만족시키는 tuple들의 집합이다.
참고로 r(R)은
해당되는 relation schema R을 따르는 tuple들의 집합이다.
1. 4번 department에서 일하는 employee의 정보를 보여줘.
2. 연봉이 30000이 넘는 employee의 정보를 보여줘.
3. 4번 department에서 일하면서 연봉이 25000보다 크거나 5번 department에서 일하면서 연봉이 30000보다 큰 employee의 정보를 보여줘.
각 조건에 맞게 DBMS가 tuple을 check해서 가져오거나 버린다. 가져온 tuple들의 결과는 table이다.
◆ PROJECT Operation
▪ Format $\pi_{<attribute$ $list>}(R)$
table에서 tuple들의 attribute list에 있는 일부의 attribute들만 보여줘.
기본적으로는 원래 있던 tuple이랑 같다. 여기서 기본적으로는 ? 그렇지 않을 때도 있나 ? YES!
▪ table R로부터 attribute list L에 나타난 column 즉, attribute들을 골라줘.
나머지 attribute들은 무시한다.
▪ 결과로 나타나는 tuple들은 attribute list L에 나타나는 특정한 attribute들만 갖는다.
▪ 원래 tuple이 100개 있었다면 기본적으로는 100개가 다 나타나야 하지만 tuple의 수가 줄어들 수 있다.
왜냐하면 PROJECT operation의 결과는 100개 중 중복된 결과들이 있으면 그 중 하나만 표현하기 때문이다.
distinct tuples들로만 구성된다.
ex) 이름, 연봉 attribute를 가지고 있고 그 중 연봉으로 project한다고 하자.
salary가 같은 사람들이 있었다면 중복되는 tuple이 생기는 것이다. 하지만 table은 중복을 허용하지 않아서 중복된 tuple들은 하나만 남기고 지워준다. 따라서 실제로 tuple의 수가 줄어들 수 있다.


project operation sign인 $\pi$가 있고 Employee라는 table에 대해서 Lname, Fname, Salary만 가지고 project하겠다는 얘기이다.
이번에는 성별과 연봉에 대해 project해보자. 그랬더니 tuple이 7개로 줄었다. 이는 성별과 연봉이 같은 사람이 존재하기 때문에 하나가 지워진 것이다.
중복이 왜 생길까?
없어진 attribute에 의해 구분되었던 tuple이 project에 의해 attribute이 없어졌기 때문에 중복이 생기는 것이다.
◆ Relational Algebra Expressions
▪ relational algebra operations들을 연속적으로 적용할 수 있다.
▪ 이로써 좀 더 복잡한 query를 나타낼 수 있다.
- relational algebra expression으로 나타낼 수 있는 이유는 결과가 relation으로 나오기 때문이다. relational algebra operation을 적용한 결과가 relation이기 때문에 또 다시 operation을 적용할 수 있다.
ex)
"Retrieve the first name, last name, and salary of all employees who work in department number 5"
$\pi_{Fname, Lname, Salary}(\sigma_{Dno=5}(EMPLOYEE))$
5번 department에서 일하고 있는 employee의 First name, Last name, Salary를 가져와라.
(자연어로 되어있는 query를 relational algebra로 바꿀 수 있어야 한다.)
이는 sequence of relation algebra operations를 적용한 결과이다.
- 위처럼하지 않고 각각의 중간 결과를 별도의 table name을 줘서 처리할 수 있다.
DEP5_EMPS <- $\sigma_{Dno=5}$(EMPLOYEE)
// 이렇듯 하나의 임시 테이블을 만들어서 다시 project할 수 있다. 다만 조금 번거로울 뿐이다.
RESULT <- $\pi_{Fname, Lname, Salary}$(DEP5_EMPS)
- 결과 table의 attribute name을 다시 지을 수 있다. (rename)
TEMP <- $\sigma_{Dno=5}$(EMPLOYEE)
$R$(First_name, Last_name, Salary) <- $\pi_{Fname, Lname, Salary}$(TEMP)
이렇게 되면 결과물의 table이름이 R이고 Fname -> First_name, Lname -> Last_name이 된다.
◆ Set Operations
▪ 집합 연산은 relation database가 set of tuples인 relation이기 때문에 필요하다.
1. UNION operation
▪ $R_1 ∪ R_2$
2. INTERSECTION operation
▪ $R_1 ∩ R_2$
3. SET DIFFERENCE (MINUS) operation
▪ $R_1-R_2$
4. CARTESIAN PRODUCT (CROSS PRODUCT) operation
▪ $R_1×R_2$ 가능한 모든 조합으로 구성되는 table
ex)
DEP5_EMPS $\leftarrow \sigma_{Dno=5}$(EMPLOYEE)
RESULT1 $\leftarrow \pi_{Ssn}$(DEP5_EMPS) // 5번 department에서 일하는 employee의 주민번호 집합
RESULT2(Ssn)$\leftarrow \pi_{Super\_ssn}$(DEP5_EMPS) // 5번 department에서 일하는 employee의 supervisor 집합을 RESULT2라 하고 그 attribute name을 Super_ssn말고 Ssn이라 하자. 즉, 5번 department에서 일하는 employee의 supervisor의 Ssn이다.
RESULT $\leftarrow$ RESULT1 $\cup$ RESULT2 // 중복을 제거한다.

RESULT1과 RESULT2 모두에 속한 333445555는 5번 department에 일하면서 5번 department에서 일하는 사람의 supervisor이다.
RESULT2에만 있는 888665555는 5번 department에 일하지 않지만 5번 department에서 일하는 사람의 supervisor이다.
▪ Union compatibility (type compatibility) 합집합 호환성
Q) 2개의 relation을 union하려고 할 때 아무거나 다 union할 수 있을까?
A) No.
- 2개의 relation은 같은 tuple의 type을 가져야한다.
- For set operations $∪, ∩$ and $-$
1. 두 개의 relation $R(A_1, A_2, ..., A_n), S(B_1, B_2, ..., B_n)$이 같은 수의 attribute n개를 가져야한다.
2. 각각의 대응되는 attribute pair가 비슷한 domain을 가져야한다. domain이 compatible 해야한다. attribute 이름은 달라도 된다. attribute의 domain이 완전 똑같지 않아도 된다. $A_1$의 domain이 1~100인데 $B_1$의 domain이 1~50이어도 괜찮다.
- dom($A_i$) = dom($B_i$)
이를 모두 충족해야지 의미있는 연산이 가능하다.

두 개의 relation이 union compatible한지 알아보자.
1) attribute name이 같을까?
아니다. 다만, 다르다고 해서 union compatible하지 않다고 하지 않는다.
2) attribute 수가 같을까?
attribute가 2개씩 있다. 따라서 같다.
3) 대응되는 attribute가 domain이 compatible할까?
domain이 둘다 character String이다. 따라서 compatible하다.
모든 조건을 만족하므로 이 두 relation은 union compatible하다. 따라서 union, intersection, set difference도 모두 가능하다.

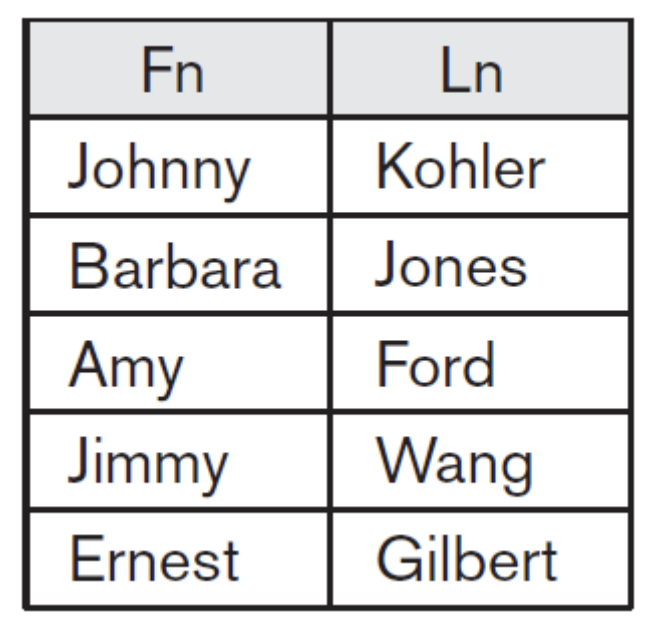
STUDENT ∪ INSTRUCTOR 결과
두 relation의 tuple을 더한 것보다 union 이후 tuple의 수가 줄어들었다. 왜냐면 중복되는 tuple이 있었기 때문에 하나를 버렸기 때문이다.
Attribute name이 Fn, Ln으로 바뀌었다. 이를 통해 첫 번째 table의 attribute name을 따랐다는 것을 알 수 있다.

STUDENT ∩ INSTRUCTOR
이 사람들로 인해 union 후 tuple 2개가 줄어든 것이다.
STUDENT - INSTRUCTOR
이는 student에 있는 tuple들 중 INSTRUCTOR에 존재하지 않는 것들만 남는다.

INSTRUCTOR - STUDENT
공통되어 있는 tuple들을 뺀다.
∩, ∪ 는 왼쪽과 오른쪽이 바뀌어도 되는데 set difference는 결과가 바뀌어서 안 된다. 즉, syemmetric하지 않다.
◆ CARTESIAN PRODUCT Operation (곱집합)
▪ Format
$R$ X $S$ // 2개의 table의 곱집할을 하면 하나의 table이 나온다.
$R(A_1, A_2, ..., A_n)$ X$ S(B_1, B_2, ..., B_m) $ // n개의 attribute을 가지고 있는 table과 m개의 attribtue을 가지고 있는 table의 곱집합
결과 테이블은 $A_1, A_2, ..., A_n, B_1, B_2, ..., B_m$의 아주 긴 attribute를 갖는다.
$k$개 tuple X $l$개 tuple = $kl$개의 tuple들로 구성된 결과가 도출된다.
▪ Meaning
- 왼쪽에 있는 table에 존재하는 각 tuple과 오른쪽에 있는 table의 모든 가능한 tuple을 combine하는 것이다.
- 결과 table $Q$: $Q(A_1, A_2, ..., A_n, B_1, B_2, ..., B_m)$
- attribute의 수: n + m
- tuple들의 수: $n_R*n_S$
- 이 자체만으로는 별의미가 없고 이 후 selection operation을 하므로써 의미있게 만들 수 있다.
▪ Example
"Retireve a list of names of each female employee's dependents"
여성 사원들의 부양가족의 이름을 알고 싶다.
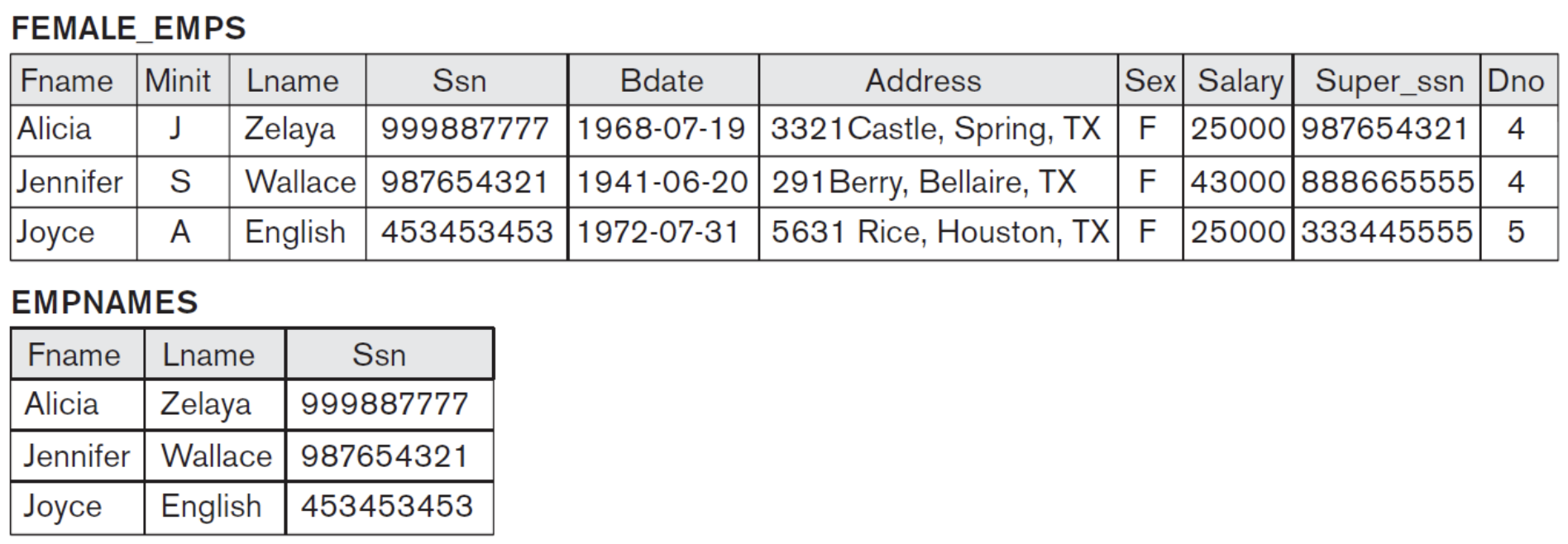
FEMALE_EMPS $\leftarrow \sigma_{Sex = 'F'}$(EMPLOYEE)
EMPNAMES $\leftarrow \pi_{Fname, Lname, Ssn)$(FEMALE_EMPS) // 여성사원의 이름과 주민번호만 가지는 테이블
EMP_DEPENDENTS $\leftarrow$ EMPNAMES X DEPENDENT // 각 여성사원이 모든 dependent들과 한 번씩 결합된다.
ACTUAL_DEPENDENTS $\leftarrow \sigma_{Ssn = Essn}$ =(EMP_DEPENDENTS)
RESULT $\leftarrow \pi_{Fname, Lname, Dependent_name}$(ACTUAL_DEPENDENTS)


◆ JOIN Operation
앞서 배운 Cartesian product는 그 자체만으로는 실질적으로 의미가 없었다. 의미를 만들기 위해서는 두 테이블의 관계를 찾아서 select하는 관계가 필요했다. Ssn = Essn 즉, PK = FK를 함으로써 서로 다른 테이블내에 있는 tuple들 간의 관계를 찾아냈다. 이때 두 번의 과정을 거쳐야하는 불편함을 해소하기 위해 만든것이 join operation이다.
▪ 서로 다른 table에 있는 tuple들간의 관계를 찾기 위해서 필요하다. 물론 join 없이도 cartesian product를 한 후에 select를 해도 되지만 이를 한 번에 하고 싶은 목적에서 나온 새로운 연산이다.
▪ Example
"Retrieve the name of the manager of each department"
각각의 department의 manager의 이름을 찾고 싶다. 이는 각 department가 어떤 employee를 manager로 가지고 있는지의 관계가 중요하다.

Department의 foreign key와 employee의 primary key가 같은 걸 찾으면 된다.
Department table과 employee table을 서로 cartesian product한 후에 Mgr_ssn = Ssn을 찾으면 위와 같은 세 쌍이 나온다.
- Using CARTESIAN PRODUCT
1. ALL_PRODUCT $\leftarrow$ DEPARTMENT X EMPLOYEE
2. DEPT_MGR $\leftarrow \sigma_{Mgr_ssn = Ssn}$ ALL_PRODUCT
3. RESULT $\leftarrow \pi_{Dname, Lname, Fname}(DEPT_MGR)
이를 단번에 어떻게 찾을까?
- Using JOIN
DEPT_MGR $\leftarrow$ DEPARTMENT $\bowtie_{Mgr_ssn = Ssn}$ EMPLOYEE // 두 테이블에서 두 attribute이 같은 쌍만 찾아줘)
RESULT $\leftarrow \pi_{Dname, Lname, Fname}(DEPT_MGR)
- JOIN operation이 필요한 이유
1. query를 작성하는 사람이 간단함
2. 처리하는 속도가 훨씬 빨라짐. cartesian product를 하기 위해서는 모든 쌍을 다 만들고 이를 모두 disk에 저장해야한다. 이 사이즈가 굉장히 크기 때문에 시간이 많이 걸린다. 하지만 위처럼 해결하면 가능한 쌍을 모두 만드는 것이 아니라 같은 쌍만을 미리 찾아서 하기 때문에 훨씬 빠르게 처리가 가능하다.
THETA JOIN Operation
▪ Format
$R \bowtie _{<join condition>} S$
R과 S간에 join condition이 만족하는 쌍을 찾아줘.
▪ Meaning
- join condition c를 만족하는 조합만 만들어서 새로운 table에 넣는다.
- cartesian product의 SELECT한 후의 결과가 같다. select에 있는 condition이 바로 join condition이다.
▪ join condition으로 쓰일 수 있는 것
- <condition> AND <condition> AND ... AND <condition>
- <condition> = $A_i \theta B_j$
- $\theta = { -, <, \leq , >, \geq , \neq }$
theta에 다양한 관계연산자를 쓸 수 있어서 theta operation이라고 부른다.
EQUIJOIN Opeartion
▪ Meaning
- JOIN operation에서 theta가 = 인 경우를 말한다.
- join 결과의 table 내에는 join attribute 2개가 모두 같다.
NATURAL JOIN Operation
EQUIJOIN을 하면 join attribute 2개가 같아서 하나의 table에 중복된 값이 들어간다. 이를 해결하기 위해 나온 operation이다.
▪ Format
$R * S$
▪ Meaning
- join attribute으로 사용되는 것들이 같을 경우를 찾아내기 때문에 결과로 나온 tuple들은 두 개의 attribute이 모두 같은 결과를 가지고 있다. 이는 자연스럽지 못하다.
- 중복된 2번 째 attribute을 날려버린다. 그래서 자연스럽게 만들겠다.
- 따라서 join을 하기 전에는 두개의 Join attribute이 반드시 같은 이름을 갖도록 한 후에 join을 해야한다.
▪ Example
“Combine each PROJECT tuple with the DEPARTMENT tuple that controls the project”
PROJECT tuple 과 그 project를 control하는 DEPARTMENT tuple의 쌍을 찾아줘.
DEPT $\leftarrow \rho_{(Dname, Dnum, Mgr_ssn, Mgr_start_date)}$(DEPARTMENT) -> 이 과정이 rename하라는 뜻이다. department에서는 dnumber로 가지고 있는데 Dnum으로 바꾸라고 시킨 것이다.
PROJ_DEPT $\leftarrow$ PROJECT * DEPT
다만, natural join operation은 join condition을 별도로 요청하지 않기 때문에 join attribute이 똑같은 이름의 attribute으로 미리 설정해야된다.

▪ Example
“Combine each DEPARTMENT tuple with its location”
Department tuple과 그의 location의 쌍을 보여줘.
DEPT_LOCS $\leftarrow$ DEPARTMENT * DEPT_LOCATIONS // 이미 둘다 Dnumber로 같은 attribute 이름을 가지고 있다.

location에 위치한 department의 name을 알 수 있게 되었다.
하나 이상의 join attribute에 의해 join이 될 수 있는데 join attribute이 달라지만 다른 table이 된다. 이는 다른 의미를 갖는다.
▪ Example
“Associate each DEPARTMENT with its manager”
DEPARTMENT $\bowtie_{Mgr_ssn=Ssn}$ EMPLOYEE
“Associate each EMPLOYEE with the department for which the EMPLOYEE works”
EMPLOYEE $\bowtie_{Dno=Dnumber}$DEPARTMENT
1. join attribute이 다르면 join 결과의 의미가 다르게 된다.
2. 같은 쌍의 table의 경우에도 서로 다른 쌍의 join이 가능하다.
하나의 table이 join 연산의 양쪽에 올 수 있다.
join을 할 때 양쪽에 같은 table의 copy가 있다고 생각하면 된다.
그리고 경우에 따라서 table의 이름을 rename할 때가 있다.
▪ Example
“Retrieve the name of each EMPLOYEE and the name of its supervisor”
각 employee의 이름과 그 사람의 supervisor의 이름을 알고싶다.
SUPERVISOR(Super_ssn, Sfname, Slname) $\pi_{Ssn, Fname, Lname}$ EMPLOYEE // employee에서 주민번호와 이름을 가져와서 rename을 했다.
TEMP $\leftarrow$ EMPLOYEE * SUPERVISOR // 여기서 join attribute는 Super_ssn이다. natural join을 TEMP에 넣는다.
RESULT $\leftarrow \pi_{Fname, Lname, Sfname, Slname}$(TMEP)
recursive relationship in ER model
◆ A Complete Set of Relational Algebra Opeartions
▪ Complete set
- 이 안에 들어가는 operation들만 가지면 어떠한 relational algebra expression도 다 표현 가능하다.
▪ Complete set of relational algebra
⚫ {SELECT, PROJECT, UNION, SET DIFFERENCE, CARTESIAN PRODUCT}
이 다섯 개만 있으면 어떠한 relational algebra expression도 다 표현 가능하
⚫ JOIN? 왜 없지?
▪ CARTESIAN PRODUCT 후 SELECT를 하면 join을 표현할 수 있다.
⚫ INTERSECTION? 교집합은?
▪ Meaning?
▪ How to express by the complete set? A - (A U B - B)
⚫ DIVISION? (out of scope)
▪ Relationally complete languages
- 어떤 query language가 새롭게 만들어 졌을 때 relational algebra operation의 complete set을 다 표현할 수 있으면 우리는 이 새로운 query language를 relationally complete language라고 부른다.
Summary
▪ Relational Algebra Operations
1. SELECT
2. PROJECT
3. Set Operations
- UNION, INTERSECTION, SET DIFFERENCE, CARTESIAN PRODUCT
4. JOIN
- THETA JOIN
- EQUIJOIN
- NATURAL JOIN